Edges to edges

This article will introduce a way to generalize graphs, giving rise to a handful of novel structures with interesting uses. They will allow for a very intricate and compact representation of knowledge or provide a different way of looking at things.

Overview and terminology

First, we will explore the idea of allowing edges from nodes to edges. This new kind of connection - going from a node to an edge - we'll name a ⊤-edge because of its appearance. If you're working with directed edges, it has a dual: the ⊥-edge, connecting an edge to a node. Next, we will look into connecting edges to other edges, naming them H-edges. Finally, drawing a high-level picture of how these extensions can embed directed hypergraphs and be embedded in metagraphs.

Because of the duality, this article will only discuss T-edges (denoted with the letter for ease of notation). We'll name the structures that arise from these connection types and combinations thereof after their most general constituent. G's abbreviate graphs (together with G-edges for regular edges), T's are graphs extended with T-edges, H's allow all edge types. Sometimes it's helpful to write things out in text rather than draw them in H-Edit. Therefore, I'll denote an edge from entity a to entity b as (a → b).

T's

As a motivating example, let's draw a T-edge from a node to an edge and say that edge gains the meaning of the connected node. For instance, if there's a G-edge from "Alice" to "Bob" and a T-edge from the node "Likes" to that, then this construction can be read as "Alice likes Bob". We can expand upon the previous example by adding a node "For this example" and draw a T-edge from this node to our existing T-edge. The entire construction now reads: "Alice, for this example, likes Bob". Note that the last T-edge connects to a T-edge; it is often practical to only allow the first-order construction.

The relationship between Alice and Bob can be further specified by adding more properties. We will add nodes "in general", "just here", "really", and "hates" and construct the following T.

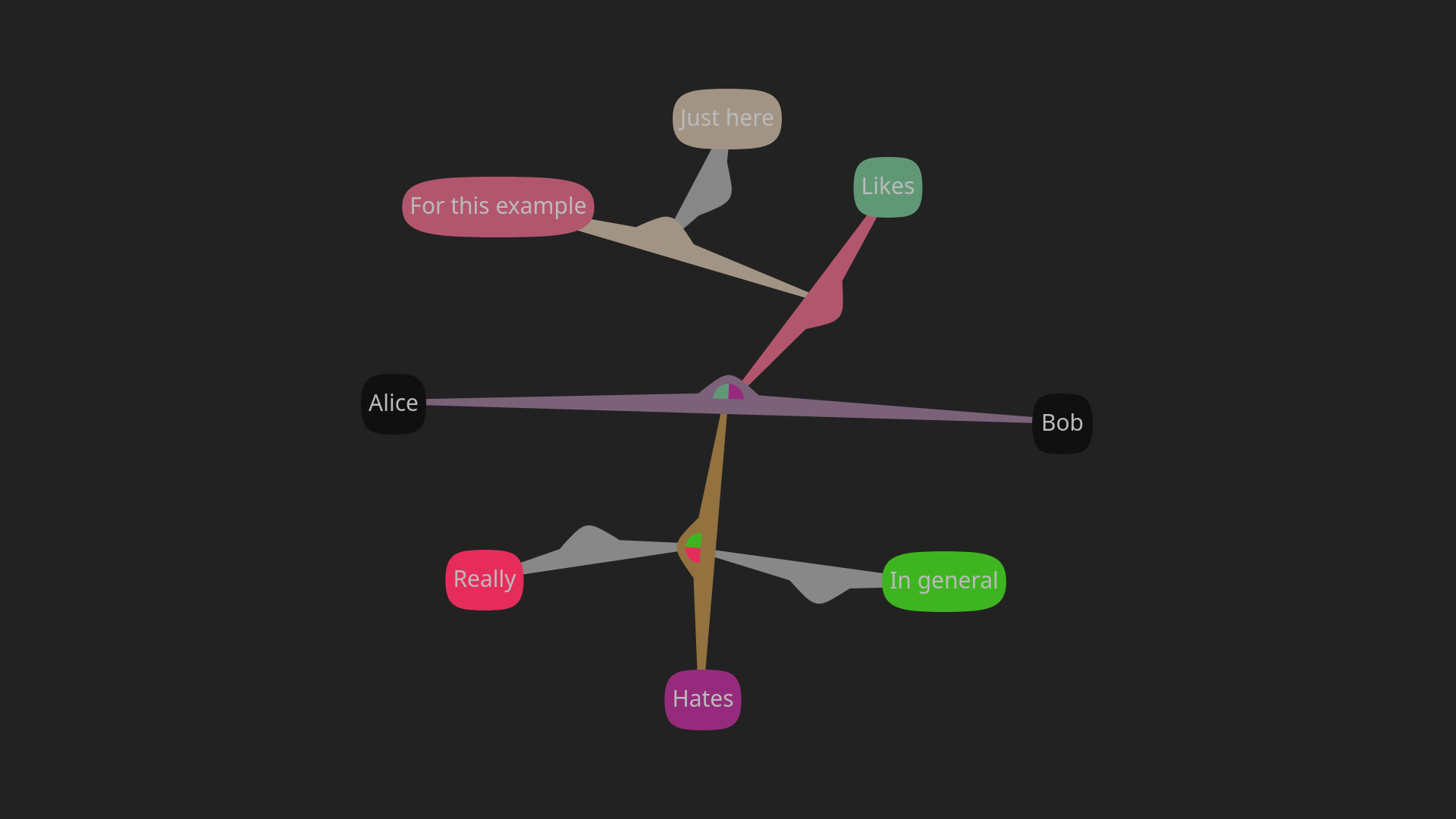The above T can be read as "Alice in general, really hates Bob and just here for this example likes Bob".

H's

A question one might ask is: "what happens when you draw an edge from an edge to another edge?". This edge could take the form of the central arrow in (a → b) → (x → y). Connecting two edges with an H-edge - similarly to connecting two nodes with an edge, and in contrast with T-edges - does not intrinsically add information beyond the connection itself. To add extra structure, H-edges can be tagged by nodes with T-edges. Furthermore, T-edges can be connected by an H-edge, which then can be tagged by a ⊥-edge forming more complex expressions like ((xy → (x → y)) ↔ (ab → (a → b))) → s.

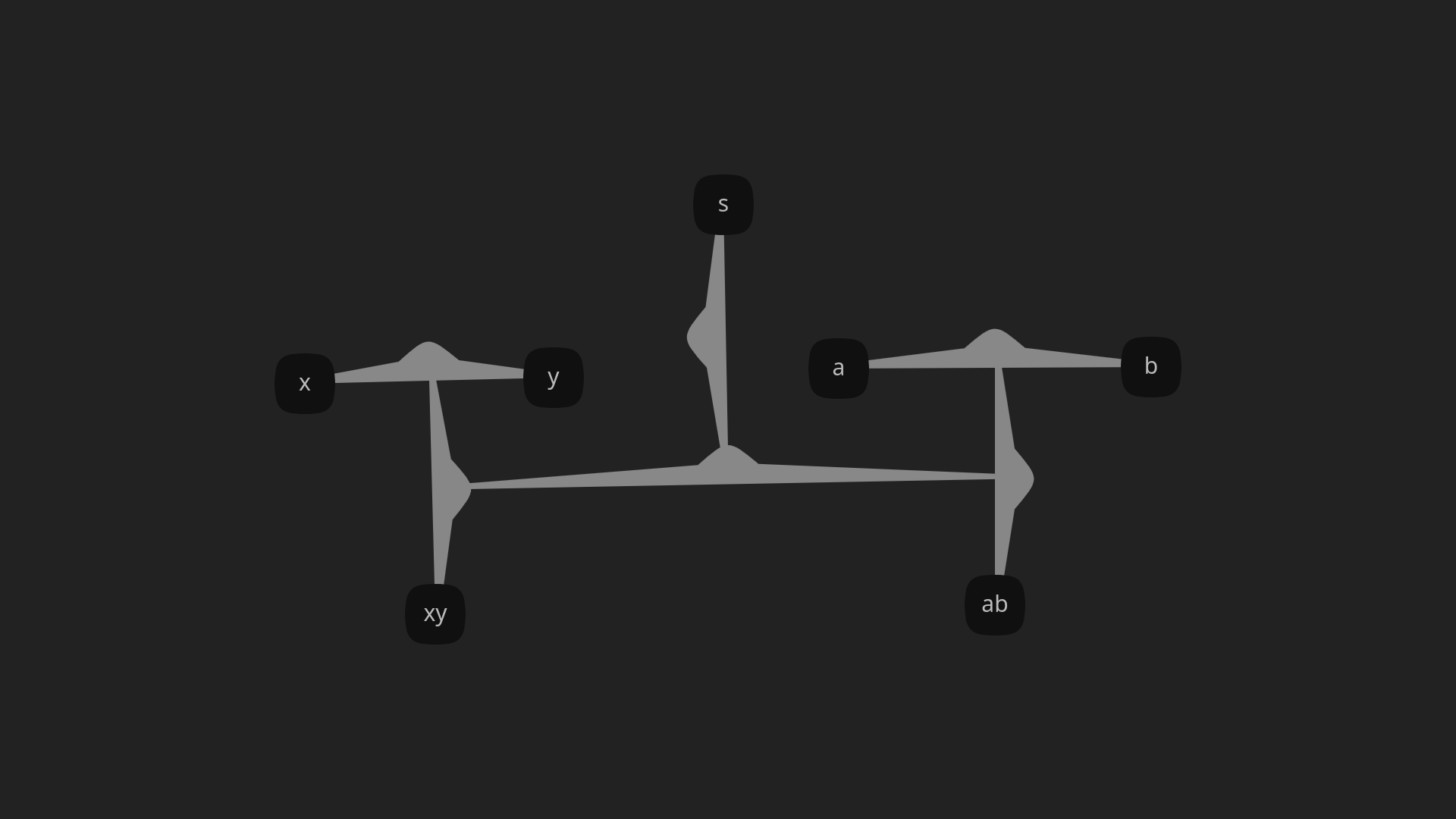
Combining these different generalizations yields a flexible and descriptively powerful datastructure. Let's look at an example taken from GEB, the semantic network. You can explore the example freely below using the arrow keys.

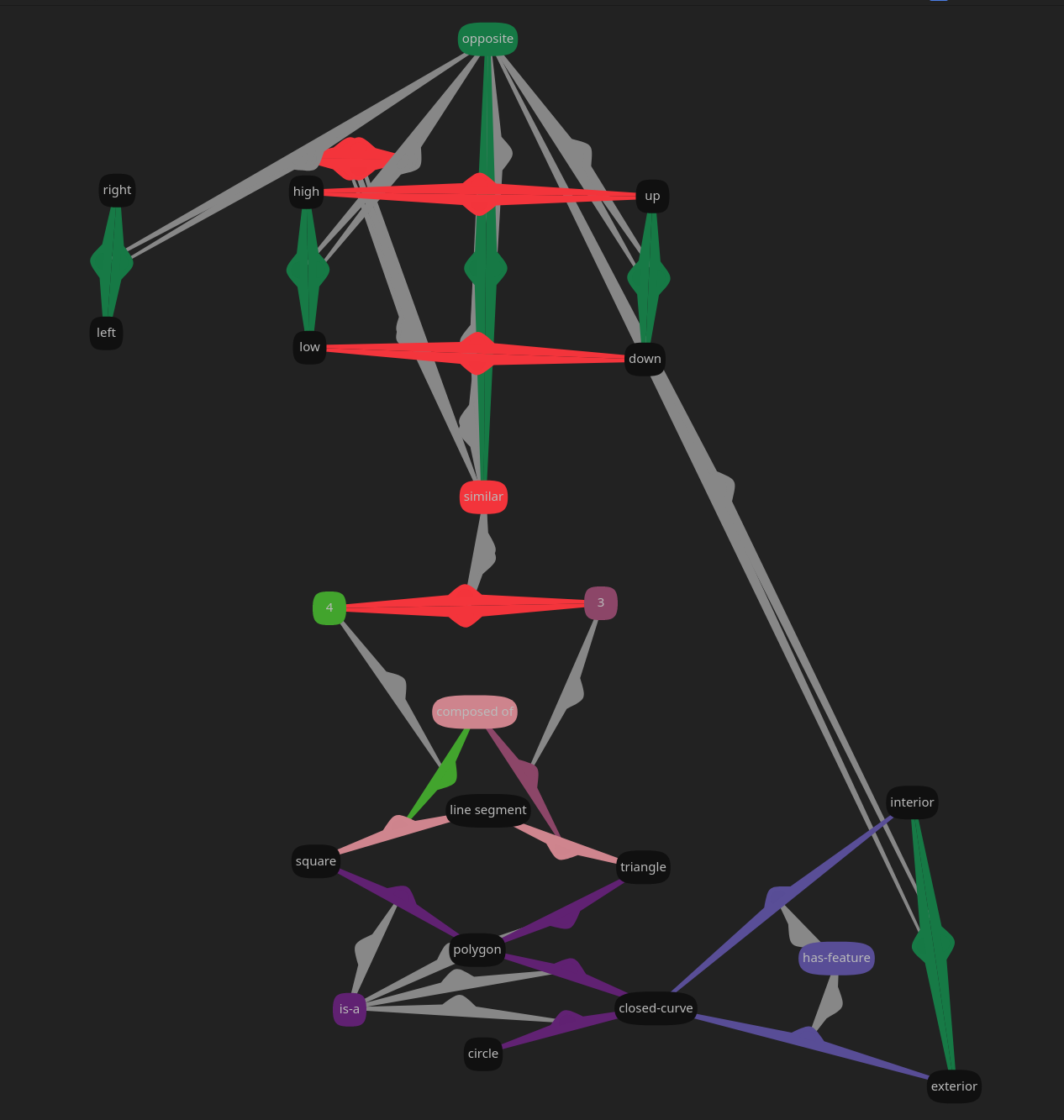
Relation to other formalisms

When we generalize graphs such that edges can connect multiple nodes, we call these hypergraphs. Hyperedges can be seen as a bag of nodes and see many applications. For example, if the nodes represent tweets, a hyperedge can represent a specific hashtag and connect all tweets using it. We can define a directed hypergraph to use (ordered, for example, by date) tuples of nodes instead of sets of nodes as edges. Together with graph-rewriting, this gives rise to complex dynamics, which I will address in a future article.

Let's associate the Alice and Bob T with its corresponding directed hyperedge. When we use arrows to represent edges, we get (for-this-example → (likes → (Alice → Bob))). Remember, we do not allow constructions like (x → ((a → b) → p)) in T's because there is a ⊥-edge from (a → b) to node p. Thus a chain of T-edges can always be written as a tuple by flattening the expression. For this example, the tuple is (for-this-example, likes, Alice, Bob), a valid directed hyperedge.

We can generalize (directed) hypergraphs further (confusingly called generalized hypergraphs by Wikipedia) by allowing hyperedges to contain other hyperedges. This structure represents an S-expression with nodes as atoms when expanded. An example would be (links (concept a) (name a) (function a)).

H's are S-expressions in this way: ((xy → (x → y)) ↔ (ab → (a → b))) → s is just a tree with arity two and nodes as leaves. Expanding the bidirectional edge and replacing the arrows, we get two S-expressions, one of which is (((xy (x y)) (ab (a b))) s).

Another related formalism is that of the Higraph, where nodes can contain other nodes inside them. H-edges can instantiate nodes by containing their classical source and edge nodes while allowing connections to other edges.